The Method of Nearby Problems

The Method of Nearby Problems, or MNP, has been under development since 2003

• While there are many potential uses of MNP, the two primary uses are: for the generation of exact solutions to complex equations and as a single grid numerical error estimator
• The basics steps of MNP include an initial numerical solution, a curve fit to that solution, then operation of the governing equations onto the curve fit to generate small source terms
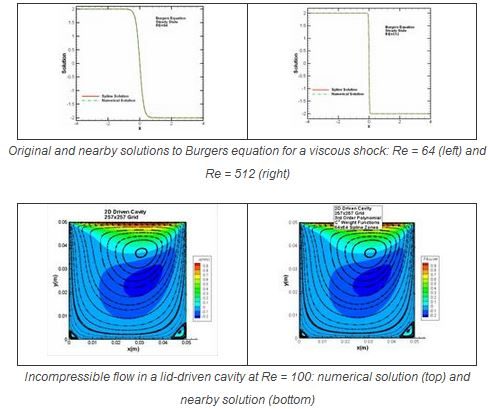
• Successful 1D MNP applications include high Reynolds number viscous shocks
• Successful 2D MNP applications include steady-state heat conduction and the flow in a lid-driven cavity (i.e., incompressible Navier-Stokes equations)
• Collaborators: Dr. Matt Hopkins of Sandia National Labs and Dr. Andrew Sinclair of Auburn University

MNP Examples

References

• C. J. Roy and M. M. Hopkins, "Discretization Error Estimates using Exact Solutions to Nearby Problems," AIAA Paper 2003-0629, invited paper for session on Uncertainty in CFD, Reno, NV, Jan. 6-9, 2003.
• M. M. Hopkins and C. J. Roy, "Introducing the Method of Nearby Problems," European Congress on Computational Methods in Applied Sciences and Engineering, P. Neittaanmaki, T. Rossi, S. Korotov, E. Onate, J. Periaux, and D. Knorzer (eds.), Jyvaskyla, Finland, July 2004.
• C. J. Roy, A. Raju, and M. M. Hopkins, "Estimation of Discretization Errors using the Method of Nearby Problems," AIAA Journal, Vol. 45, No. 6, 2007, pp. 1232-1243.
• C. J. Roy and A. J. Sinclair, "On the Generation of Exact Solutions for Evaluating Numerical Schemes and Estimating Discretization Error," NATO RTO Symposium on Computational Uncertainty, Athens, Greece, Dec. 3-6, 2007.
• C. J. Roy and A. J. Sinclair, "On the Generation of Exact Solutions for Evaluating Numerical Schemes and Estimating Discretization Error," Journal of Computational Physics, Vol. 228, No. 5, 2009, pp. 1790-1802 (DOI: 10.1016/j.jcp.2008.11.008).